is multiplied by the probability of ketchup usage, then we have the joint probability of both mustard and ketchup usage:
Example: Sensitive Questions (Multiplication Rule)
Suppose that a survey was carried out in New York, and each respondent was faced with the following two questions:
a. Is the last digit of your Social Security number odd?
b. Have you ever lied on an employment application?
The second question is, of course, quite sensitive, and for various reasons we might expect that a number of people would not answer the question honestly, especially if their response was yes. To overcome this potential bias, respondents were asked to flip a coin and then to answer question (a) if the result was “head” and (b) otherwise. A “yes” response was given by 37%of all respondents. What is the probability that a respondent who was answering the sensitive question, (b), replied “yes”?
Solution: We define the following events:
A: Respondent answers “yes.”
E1: Respondent answers question (a).
E2: Respondent answers question (b).
From the problem discussion we know that P(A) = 0.37. We know that the choice if question was determined by a flip of a coin and that P(E1) = 0.5 and P(E2) = 0.5. In addition, we know the answers to question (a). Since half of all Social Security numbers have an odd last digit, it must be that the probability of a “yes” answer, given that question (a) has been answered, is 0.5—that is, P(A/E1) = 0.50.
However, we require P(A/E2), the conditional probability of a “yes” response, given that question (b) was answered. We can obtain this probability by using two results from previous sections. We know that E1 and E2 are mutually exclusive and collectively exhaustive.
From the result, we estimate that 24% of the surveyed population has lied on some employment application.
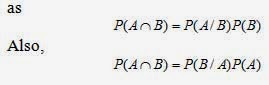
No comments:
Post a Comment